Click on the colored portions to expand or collapse content.
Reduction Modulo $p$
In this part, we will give the methods permitting the study of Galois goups of monic polynomials with integer coefficients by reduction $\mod p$. Of course, the situation over $\F_p$ is atleast theoretically very simple: we know for example the factorization of polynomials, the extensions are always Galois and Galois groups are cyclic, with canonical generator a prime, the frobenius morphism.
We are given a prime number $p$. We will compare the
Galois group of $P$
$\gal(K/k)$ where $K=k[x_1,\ldots,x_r]$ with $x_i$ roots of $P$.
denoted as $\gal(P/\Q)$ and the Galois group of $\bar{P}$ (obtained from $P\mod p$ and denoted as $\gal(\bar{P}/\F_p)$), when $\bar{P}$ is separable. Since $P$ is monic, denote $n=\deg P=\deg\bar{P}$. The principal result for us is that, under the conditions, there exists an element of $\gal(P/\Q)$, well defined upto conjugation, whose conjugation class in $S_n$ is the same as that of Frobenius in $\gal(\bar{P}/\F_p)$ (for the canonical embeddings of the galois group in the symmetric group $S_n$). The main result we want to show is the following
Theorem Let $P$ be a monic polynomial and $\bar{P}$ is separable. Then, $\gal(P/\Q)$ admits a subgroup isomorphic to $\gal(\bar{P}/\F_p)$. For all permutations in $\gal(\bar{P},\F_p)\subset S_n$, there exists a permutation in $\gal(P/\Q)\subset S_n$. In particular, if $\bar{P}$ is irreducible, there exists a cycle of length $n$ in $\gal(P/\Q)\subset S_n$.
Specialisation of Galois Group
Let $P$ be a monic separable polynomial with integer coefficients. Denote $$A=\Z[z_1,\ldots,z_n] \quad\text{where }z_i \text{ are roots of }P$$Proof Let $L$ be the splitting field of $P$, then $A$ is contained in $L$ since $z_i\in L$, and thus $K$ is contained in $L$. Furthermore, $P$ being split of $K$, we know by minimality if $L$ that $K=L$. $\qquad \blacksquare$
The fundamental observation is that all the elements of $A$ are algebraic integers.
Definition Let $B$ be a $C$ algebra. We say that $b\in B$ is integral over $C$ if $b$ is a root of a monic polynomial with coefficients in $C$.
When $B$ is a subring of $\C$ seen as $\Z$ algebra, we recover the notion of an algebraic integer.
Proof The first part is clear: if $b$ is a root of unitary polynomial of degree $d$, then $C=C[b]$ is generated by $1,\ldots, b^{d-1}$. Inversely suppose $b\in B'$ is of finite type on $C$, generated by $b_1,\ldots, b_n$. There exist $c_{ij}\in C$ such that $bb_j=\sum_ic_{ij}b_i$. Let $\alpha=c_{ij}$, then $\alpha$ is a matrix of homothety $h_b\in \text{End}_C(B')$ with ratio $b$ in $C$.
Let $P=\det(X\Ida -\alpha)$ be the characteristic polynomial of $\alpha:$ it is the unitary polynomial with root $\alpha$ (Cayley Hamilton) and thus a fortiori $h_b$. But, we also have $0=P(h_b)\cdot 1=P(b)$, showing $b$ as a root which we wanted.
Let $P=\det(X\Ida -\alpha)$ be the characteristic polynomial of $\alpha:$ it is the unitary polynomial with root $\alpha$ (Cayley Hamilton) and thus a fortiori $h_b$. But, we also have $0=P(h_b)\cdot 1=P(b)$, showing $b$ as a root which we wanted.
Proof If $x,y$ are integral over $C$, say zeros of the monic polynomials with coefficients in $C$ of degree $n,m$, both $x-y$ and $xy$ are contained in $C[x,y]$ which is generated by the monomials $x^iy^j,0\leq i\leq n,0\leq j\leq m-1$ and thus is finite type on $C$.
Norms of elements of $A$: For all complex algebraic $z$ on $\Q$, we define the norm $N(z)$ as the product of complex conjugates. If $P$ s the minimal polynomial of $z$, we have the formula
$$N(z)=(-1)^{\deg P}P(0) \quad\text{implying}\quad N(z)\in\Q $$
Proof Suppose to the contrary, we would then write $1=pa, a\in A$. Let $d$ be the number of distinct conjugates of $a$, that is the complex numbers $\sigma(a)$ with $\sigma\in\Hom_\Q(\Q[a],\C)$ and $d=\card(\Hom_\Q(\Q[a],\C))$. Since, $\Q[a]=\Q[pa]$, the complex number $pa$ has $d$ distinct conjugates $p\sigma(a)$ with $\sigma\in \Hom_\Q(\Q[a],\C)$. We deduce the formula $$N(pa)=p^d N(a). $$ On the other hand $N(pa)=N(1)=1$ leading to $N(a)=1/p^d$ which is contradiction to the fact that $N(a)\in\Z\qquad\blacksquare$.
Decomposition Groups
Let $\bar{\id{p}}$ be a non zero maximal ideal of $\bar{A}$. Its existence can be established independently from the axiom of choice (utilizing for example that $\bar{A}$ is a vector space of finite dimension on $k$, since $A$ is finite type on $\Z$). Let $\id{p}$ be the inverse image in $A$, in other words kernel of the canonical surjection $$A\twoheadrightarrow \bar{A}\twoheadrightarrow \bar{A}/\bar{\id{p}}=k.$$ Since $p$ is non zero in $\bar{A}=A/pA$, we get $\Char k=p$.
Remark It is useful to observe that we have $\id{p}\cap\Z=p\Z$, simply because $\id{p}\cap\Z/p\Z$ is kernel of the morphism $\F_p=\Z/p\Z\ra A/\id{p}$ which is an injective map, as all morphisms of fields are injective.
Since $\bar{A}$ is of finite dimension over $\F_p$, the extension $k/\F_p$ is finite and galois, as are all extensions of finite fields. Just as $A$ is generated by the monomials in $z_i$ with coefficients in $\Z$, similarly $K$ is generated by monomials in the $x_i=z_i\mod\id{p}$ with coefficients in $\F_p$. In other words, $k$ is the field of decomposition of $\bar{P}$ on $\F_p$, which, in passing, gives a new proof of that $k$ is finite dimensional over $\F_p$.
The galois group $G=\gal(K/\Q)$ permutes $z_i$ thus leaves $A=\Z[z_1,\ldots,z_n]$ stable.
Definition. The subgroup of $G=\gal(K/\Q)$ fixing $\id{p}$ is called the group of decomposition of $\id{p}$ and is denoted as $D=D_\id{p}$.
Proof As the action of $D$ on $A$ leaves $\id{p}$ globally invariant, it defines an action on the quotient $k=A/\id{p}$. An element $\sigma_0\in\gal(k/\F_p)$ is determined by the image $y=\sigma_0(x)$ of the generator $x\neq 0$ of the extension $k/\F_p$.
The ideals $g^{-1}(\id{p})$ are equal to $\id{p}$ if and only if $g\in D$. However, the projection $A\xra{g}\ra A\ra A/\id{p}$ is surjective because $g$ is bijective and admits $g^{-1}(\id{p})$ as a kernel. Hence, we have an isomorphism. $$A/g^{-1}(\id{p})\simeq A/\id{p} $$ assuring that $g^{-1}(\id{p})$ is maximal since the quotient corresponds to the field $A/\id{p}$. In fact, it is not difficult to prove that the non zero prime ideals of $A$ are maximal, but we will not need it.
Denote by $\id{q}_1,\ldots,\id{q}_r$ be the distinct ideals of the form $g^{-1}(\id{p}),g\notin D$. As $\id{q}_0=\id{p},\id{q}_1,\ldots,\id{q}_r$ are pairwise distinct and maximal, we have $\id{q}_i+\id{q}_j=A$ if $i\neq j$. From the chinese lemma, we can thus find $z\in A$ such that $$z\equiv x\mod\id{q_0}\text{ and }z\equiv 0\mod\id{q}_i, i>0 $$ and thus $$z\equiv x\mod\id{p}\text{ and }z\equiv 0\mod g^{-1}(\id{p})\text{ if }g\notin D$$ We have then $g(z)\in\id{p}$ if $g\notin D$. The polynomial $$\prod_{g\in G}(X-g(z)) $$ has integer coefficients, the coefficients being invariant under $G$ and integral on $\Z$. By construction, its image in $k[X]=A/\id{p}[X]$ is written as $$\prod_{g\in D}(X-\bar{g(z)})\prod_{g\in D}X $$ and roots $\bar{z}=x$. Since $x\neq 0$, we deduce that the polynomial of $\F_p[X]$ $$\prod_{g\in D}(X-\bar{g(z)}) $$ is divisible by the minimal polynomial of $x$ on $k$ $$\prod_{\sigma\in\gal(k/\F_p)}(X-\sigma(x)),$$ and thus there exists $g\in D$ such that $\sigma_0(x)=\bar{g(z)}$, which we wanted to show. $\qquad \blacksquare$
The ideals $g^{-1}(\id{p})$ are equal to $\id{p}$ if and only if $g\in D$. However, the projection $A\xra{g}\ra A\ra A/\id{p}$ is surjective because $g$ is bijective and admits $g^{-1}(\id{p})$ as a kernel. Hence, we have an isomorphism. $$A/g^{-1}(\id{p})\simeq A/\id{p} $$ assuring that $g^{-1}(\id{p})$ is maximal since the quotient corresponds to the field $A/\id{p}$. In fact, it is not difficult to prove that the non zero prime ideals of $A$ are maximal, but we will not need it.
Denote by $\id{q}_1,\ldots,\id{q}_r$ be the distinct ideals of the form $g^{-1}(\id{p}),g\notin D$. As $\id{q}_0=\id{p},\id{q}_1,\ldots,\id{q}_r$ are pairwise distinct and maximal, we have $\id{q}_i+\id{q}_j=A$ if $i\neq j$. From the chinese lemma, we can thus find $z\in A$ such that $$z\equiv x\mod\id{q_0}\text{ and }z\equiv 0\mod\id{q}_i, i>0 $$ and thus $$z\equiv x\mod\id{p}\text{ and }z\equiv 0\mod g^{-1}(\id{p})\text{ if }g\notin D$$ We have then $g(z)\in\id{p}$ if $g\notin D$. The polynomial $$\prod_{g\in G}(X-g(z)) $$ has integer coefficients, the coefficients being invariant under $G$ and integral on $\Z$. By construction, its image in $k[X]=A/\id{p}[X]$ is written as $$\prod_{g\in D}(X-\bar{g(z)})\prod_{g\in D}X $$ and roots $\bar{z}=x$. Since $x\neq 0$, we deduce that the polynomial of $\F_p[X]$ $$\prod_{g\in D}(X-\bar{g(z)}) $$ is divisible by the minimal polynomial of $x$ on $k$ $$\prod_{\sigma\in\gal(k/\F_p)}(X-\sigma(x)),$$ and thus there exists $g\in D$ such that $\sigma_0(x)=\bar{g(z)}$, which we wanted to show. $\qquad \blacksquare$
Proof Denote $x_1,\ldots, x_n$ as reduction $\mod\id{p}$ of the roots $z_1,\ldots,z_n$ of $P$, thus $x_i$ are distinct. In other words the map $z_i\mapsto x_i$ is bijective inducing an identification of the group of permutations $$\Sigma(z_i)=\Sigma(x_i).$$ We have a diagram
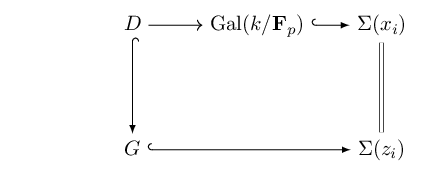
Remark The proof of the lemma gives a bit more, when the hypothesis are verified. If we have a permutation of roots of $\bar{P}$, there exists a permutation of roots of $P$ of the same type. In particular, if $\bar{P}$ is irreducible, there exists a cycle of length $n$ in $G$.
Finally, notice that, despite appearances, the sub group $D=D_\id{p}$ depends very little on $\id{p}$ but depends rather on $p$. Let us therefore, pick two maximal ideals $\id{p},\id{q}$ of $A$, such that $A/\id{p}\simeq A/\id{q} \simeq\F_p$.
Proof For the first part imagine that we have $\id{p}\not\subset g(\id{q})$ for all $g\in G$. We then have $\id{p}+g(\id{q})=A$ for all $g$ since $\id{p}$ is maximal. The chinese lemma allows to then choose $x\in A$ such that $$x\equiv 1\mod g(\id{q})\text{ for all } g$$ and $$x\equiv 0\mod\id{p}. $$ The norm of $x$ is given as $\prod_{g\in G}g(x)$ is on the one hand in $p\Z=\id{p}\cap\Z=\id{q}\cap \Z$. It is therefore also in $\id{q}$ and thus one of the factors $g(x)$ is in $\id{q}$, in other words $x\equiv 0\mod g^{-1}(\id{q}),$ a contradiction.
For the second part note that $D_{\id{p}}=D_{g(\id{q})}=gD_{\id{q}}g^{-1}$, the first equality is the first part and the last equality comes from the fact that $D_{g(\id{p})}$ fixes $g(\id{p}$), and thus composing with $g,g^{-1}$ will not impact it.$\qquad \blacksquare$
In particular $D_{\id{p}}$ and $D_{\id{q}}$ are isomorphic (via the interior automorphism $h\mapsto ghg^{-1}$, even if $G$ is abelian). In particular, the element of Frobenius defines an element of $G$ well defined upto conjugation, and well defined anyway if $G$ is abelian.
A substantial part is a translation of INTRODUCTION À LA THÉORIE DE GALOIS by Yves Lazlo.